Understand Tensors and Matrices

Before machine learning and deep learning become super popular, Tensor is more of a Physics concept. In this case, tensor refers to high dimensional matrices (plural for matrix). Let’s start with a normal number, a scalar, like 1. It’s zero dimension.

For the sake of understanding deep learning, for beginners, simply put: Tensors are just high dimensional matrices. Usually it is a stack or pile of matrices that have more than just two dimensions (width and height), now has depth (and even more dimensions), each depth layer is a matrix. In contrast, each matrix has a row or column vector, each vector is consisted of scalar numbers.

Each tensor is one or more stacks of matrices. Each matrix is a stack of rows and columns vectors. Each row or column vector is a stack of numbers.

One dimensional matrix is also known as vectors. Here’s a row vector:

import numpy as nprow_vec = np.array([0,1,2,3]) #row_vec.shape -> (4,)

Here’s a column vector:

import numpy as npcol_vec = np.array([[0],[1],[2],[3]]) -> col_vec.shape -> (4, 1)

How about a two dimension tensor? That’s simply a matrix. A large matrix looks like an excel sheet. Here’s a small 2x2 matrix.

matrix = np.array([[1,2],[3,4]]) # matrix.shape -> (2,2)

Generally tensor refers to higher dimensional matrices like the RGB value of each pixel in an image. Each pixel has an x,y coordinate (x,y) for its horizontal location and vertical location in an image. It also has three additional values: red, green, blue.

See the above image REPOST for visualization of column vector, or just vectors, matrix and tensor.

Given the above visualization technique. You can visualize an image tensor has a width, height, and the depth is usually three, one for red, one for green and one for blue.

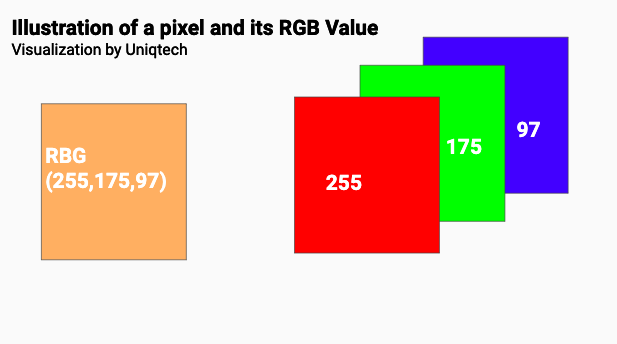
Illustration of a Pixel and its RGB value

An illustration of a tensor that represents 3 pixels in a row of the RGB value [255,175,97] corresponding to red green blue

Does the name tensor sound familiar? Yes, Google’s Deep Learning framework Tensorflow is named for tensors flowing through computational graphs.